De 7 Quality Tools – ook wel bekend als de 7 Basic Quality Tools of de 7 Quality Control Tools – vormen samen een set van verbetertechnieken die voor het eerst werden gepresenteerd door Kaoru Ishikawa in 1985. De toolset is onder meer verspreid door de ASQ en beschreven in de PMBoK guide1 van het Project Management Instituut. De tools maken deel uit van de gereedschapskist van gecertificeerde projectmanagers PMP®2 en worden gebruikt om processen te verbeteren en kwaliteit van producten en diensten te waarborgen. In dit artikel bespreek ik ze en geef aan, zoveel mogelijk met voorbeelden uit mijn eigen praktijk, op welke manier we gebruik maken van data en ook in welke situaties we de tools kunnen toepassen.
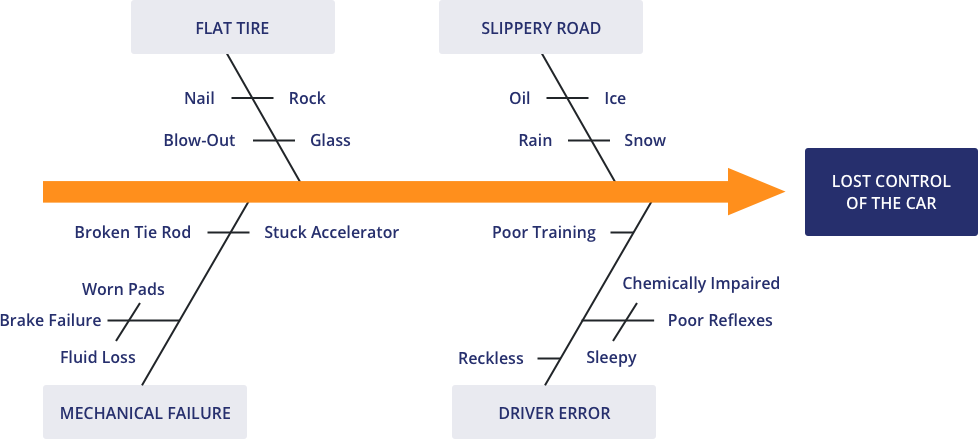
Dit diagram, ook wel bekend als het visgraatdiagram of het ‘cause-and-effect-diagram’ is genoemd naar de bedenker ervan, Kaoru Ishikawa. Hij ontwikkelde dit bij de Kawasaki Motor Company om complexe problemen in kaart te brengen. Welke oorzaken (causes) leiden tot een (meestal) negatief effect?
Het is dus een typisch analyse-instrument dat inmiddels een van de meest gebruikte is uit de set, zowel bij productiebedrijven als bij administratieve organisaties. Niet voor niets, denk ik, is dit daarom de eerste tool die beschreven wordt in het boek ’111 Instrumenten voor kwaliteitsverbetering’3 in de Analyze-fase.
Bij een complex probleem zijn er vaak meerdere (mogelijke) oorzaken te vinden die met behulp van deze aanpak gestructureerd in kaart worden gebracht. Vervolgens worden ze gecategoriseerd en worden de oorzaken idealiter allemaal, van grootste naar kleinste, weggenomen door middel van verbeteracties. Zowel de analyse als de verbeteracties worden in principe uitgevoerd door de medewerkers zelf die bij de problematiek betrokken en/of in het betreffende proces werkzaam zijn.
De rol van data is uiteraard essentieel bij dit instrument. Allereerst, hebben we een probleem? Probeer op voorhand dit probleem zo goed mogelijk te definiëren: hoe vaak komt het voor, wat is de impact en hoeveel last hebben onze klanten ervan? Soms zorgt doorvragen ervoor dat een team besluit dat het probleem eigenlijk wel meevalt en dat de energie beter gericht kan worden op andere problemen.
Ten tweede, zijn alle (mogelijke) oorzaken te kwantificeren? Vaak is nader onderzoek nodig om dit te doen zodat je weet of het zinvol is om juist deze oorzaak ook concreet aan te pakken. Ook hier geldt: je kunt jouw verbeterkracht maar een keer inzetten!
En tenslotte kan je bij het kiezen van de meest geschikte oplossing soms heel goed data en/of statistiek inzetten.
N.B. Je kunt de visgraatanalyse ook positief inzetten. Mijn goede vriend Theo van den Eijnden doet dit regelmatig vanuit zijn positieve Appreciative Inquiry aanpak waarbij je juist uitgaat van wat wel goed gaat!
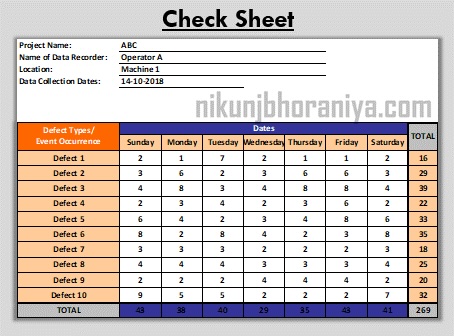
Eigenlijk is dit ‘gewoon’ een turfstaatje. Of, iets formeler, een gestructureerd, specifiek op de situatie aangepast formulier voor het verzamelen en analyseren van gegevens. Het is een generieke tool die in tal van situaties kan worden toegepast.
Het belang van dit instrument moet niet worden onderschat. Veel gegevens zijn niet uit systemen te halen en dan is het ouderwetse turven een uitstekende manier om data te verzamelen. Deze techniek heeft niet voor niets de top 7 van de Quality tools gehaald en ik gebruik het nog steeds op plekken waar de informatievoorziening laag is.
Vaak liet ik aantallen c.q. voorraden (elektronische) dossiers met verschillende status turven: nog niet opgepakt, wachten op reactie, klaar om beoordeeld te worden. Maar ik heb het ook gebruikt om te laten turven hoe vaak er verstoringen waren tijdens het werk (met een aantal vooraf benoemde categorieën, vragen van collega’s scoorden erg hoog!) De website van ASQ5 geeft nog veel meer voorbeelden van gebruik: frequentie of patronen van gebeurtenissen, problemen, defecten, locatie of oorzaken van defecten en soortgelijke problemen.
Een proces wordt zelden op exact dezelfde manier, in hetzelfde tempo, met dezelfde kwaliteit uitgevoerd. Er is variatie in de output. Vergelijk het met het lezen van een boek, gemiddeld doe je misschien 2 minuten over een pagina maar alles tussen de 1,5 en 2,5 minuut valt dan binnen de normale procesvariatie. Wiskundigen laten vervolgens statistiek op het proces los en spreken dan van ‘variantie’.
De wiskundige zegt dan ‘alles tussen 1,5 en 2,5 minuut valt binnen de zogeheten ‘regelgrenzen’, er is dus sprake van een normale procesprestatie6.
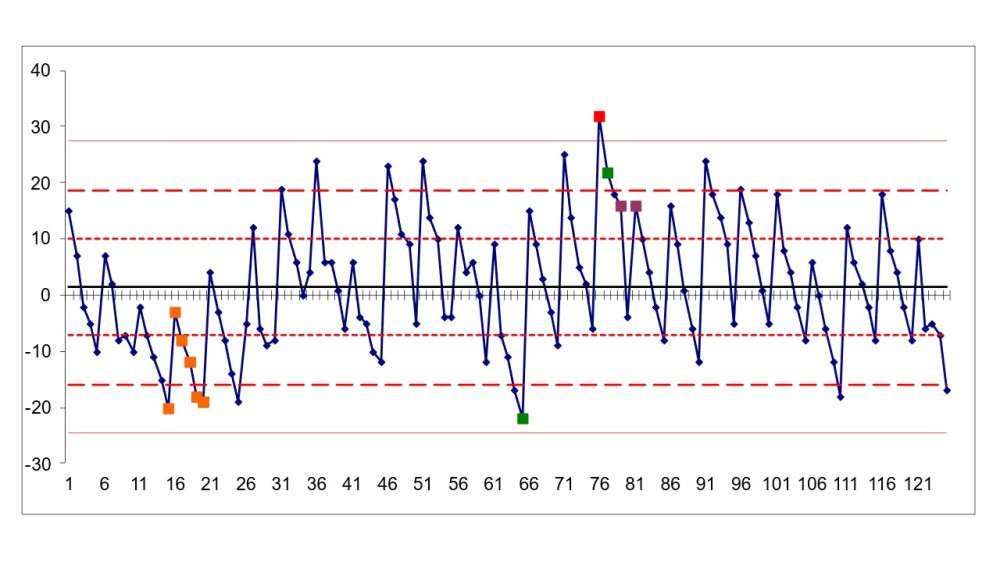
De control chart – ook wel regelkaart genoemd - is een grafiek die wordt gebruikt om de prestaties van een proces te monitoren. De grafiek toont de variatie in het proces en stelt de gebruiker in staat om te bepalen of het proces ‘in control’ is of niet doordat je er
trends, patronen en veranderingen mee kunt opsporen (bijvoorbeeld vóór en ná een verbetering).
Door de metingen achter elkaar in beeld te brengen en in een statistisch model te gieten zie je een patroon in de tijd ontstaan. Alles tussen de buitenste rode lijnen valt binnen de ‘regelgrenzen’ dus binnen de normale variantie. De gekleurde blokjes geven extra informatie omdat daar, statistisch gezien, iets bijzonders aan de hand kan zijn.
Voor de fijnproever daarom nog een toelichting op de gekleurde blokjes:
Zoals altijd moet je heel goed checken of jouw invoer klopt. Het rode blokje in de tabel zou bijvoorbeeld ook een foute meting kunnen zijn. Zeker als er sprake is van handmatige invoer is een fout snel gemaakt. Zo had een collega een zeer rare meting bij de duur van een bepaalde handeling. Toen bleek dat er 1 meting totaal uit de kaart schoot, omdat degene die deze meting had gedaan, tijdens het uitvoeren van haar proces tussendoor haar collega’s had getrakteerd op gebak. Dit verstoorde uiteraard ook het gemiddelde van het proces (dat doorgaans een minuut duurde) gigantisch. Meestal gebruik je als input continue gegevens zoals lengte, gewicht, tijd, temperatuur, etc.
Een histogram is een grafiek die wordt gebruikt om de frequentieverdeling van een dataset weer te geven. Het toont hoe vaak elk datapunt voorkomt in de dataset en zegt dus iets over de verdeling van de gegevens.
Stel, ik laat iemand zonder liniaal strookjes knippen die exact 10 cm breed moeten zijn met een maximale foutmarge van 4%7. Ernaast zit een persoon die alleen terugkoppelt ‘te breed’ of ‘te smal’. Vervolgens moet die persoon over een berekende bandbreedte de strookjes boven elkaar leggen. Het resultaat ziet er dan als volgt uit:
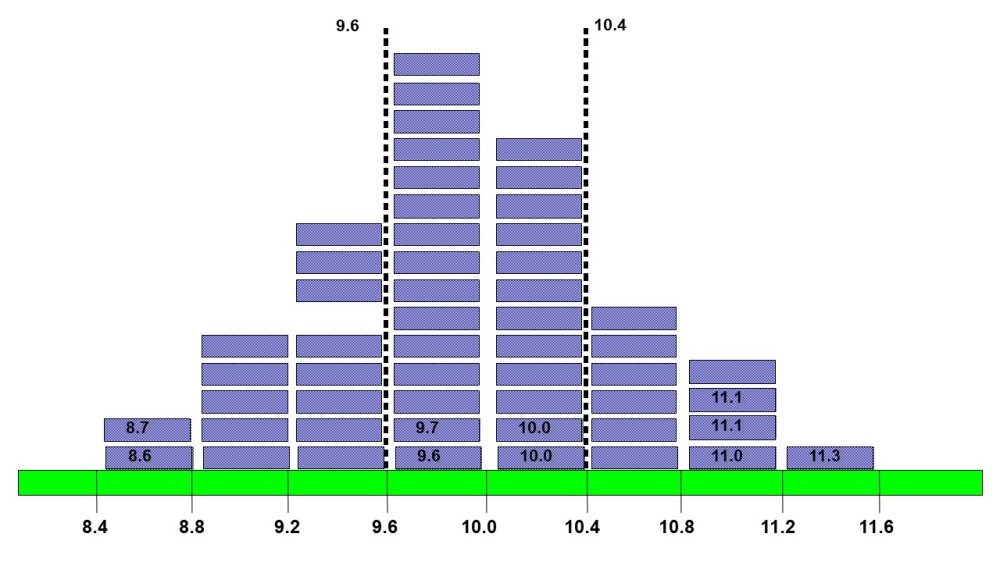
Dit is dus een histogram, vele lezers zullen ‘m wel kennen. In dit voorbeeld zijn de klassenbreedte en -grenzen (8.4 t/m 11.6) door de opsteller vastgesteld om goed te laten zien wat precies binnen de kaders van de klantwens (tussen de 9.6 en 10.4) valt. Bij een dataset kan je deze grenzen ook door bijvoorbeeld Excel laten berekenen.
In het kader van dit instrument wil ik het bij data vooral hebben over de output. Analyse met behulp van het histogram geeft inzicht in de centrale tendens, de spreiding en eventuele uitschieters. Om een voorbeeld te noemen, bij het voorbeeld over de geknipte papierstrookjes zou je een normaalverdeling verwachten zoals hieronder:
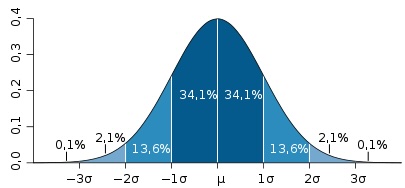
In de praktijk van het strookjesknippen is dat vrijwel altijd ook het geval.
Echter, bij andere processen waar je hetzelfde zou verwachten is dat niet altijd het geval. Kijk bijvoorbeeld eens naar de doorlooptijd van een claim die ik bij een bedrijf in kaart bracht. Hieronder zien we een aantal bijzonderheden.
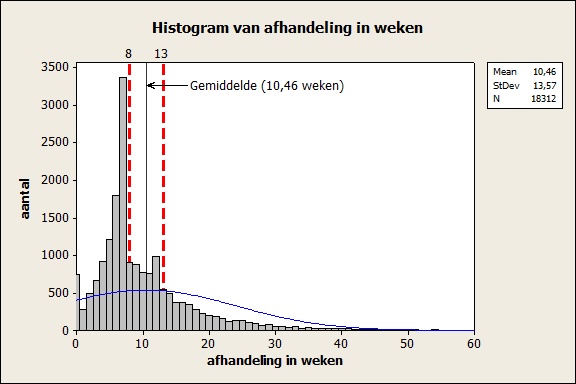
Dit lijkt niet erg op een normaalverdeling:
• Er zijn 3 pieken, een op 0 weken, een op 7 weken en een op 12 weken
• De piek van 7 weken is extreem hoog
• Er is een hele lange uitloop naar 60 weken
Wat is hier aan de hand?
Het antwoord is grotendeels te verklaren uit gedrag. Er werd door het management van deze organisatie – even kort door de bocht – uitsluitend gestuurd op de prestatie-indicator doorlooptijd. Wat betekent dat? Bij een PI ‘binnen 8 weken’ laten we de dossiers liggen terwijl ze allang afgehandeld kunnen worden, tot de 7e week, en dan werken we ze massaal weg.
Gedurende een korte tijdsspanne was de PI niet 8, maar 13 weken geweest, wat het piekje van week 12 verklaart. De piek bij 0 weken werd verklaard doordat er relatief veel claims binnenkwamen voor de claimdatum, die al voorafgaand aan het recht op uitbetaling beoordeeld waren (niet alle claimbehandelaars lieten de dossiers zo lang mogelijk liggen). De lange uitloop naar 60 weken heb ik niet onderzocht, er zou ook daar sprake kunnen zijn van gedrag, maar mogelijk ook van zeer complexe situaties.
N.B. Enige tijd na mijn onderzoek is de betreffende organisatie gaan sturen op ‘zo snel mogelijk’ als PI, ik verwacht dat als ik dezelfde meting opnieuw zou laten uitvoeren, ik een veel betere normaalverdeling zou zien.
We kunnen met dezelfde dataset ook iets zeggen over de Cp-en/of Cpk-waarde8 (de ‘capability’ van het proces) met andere woorden in hoeverre valt het proces binnen de specificatielimieten c.q. de eisen die de klant eraan stelt? In het eerste plaatje zie je goed de resultaten tussen de waardes 9,6 en 10,4 maar je moet nog wel even tellen hoeveel procent dan goed is. Statistiekprogramma’s rekenen feilloos uit of je goed bezig bent en belangrijker, of je aan de slag moet met verbeteren van je proces of niet. Vrijwel altijd wel dus 😉.
Vilfredo Pareto (1848 – 1923) kwam erachter dat 80% van de bezittingen in Italië in handen waren van 20% van de populatie. Later heeft Joseph Juran (1904 – 2008) deze observatie veralgemeniseerd en geformuleerd dat in het algemeen 20% (the vital few) van de oorzaken verantwoordelijk is voor 80% van de problemen.
Het is belangrijk op te merken dat de 80-20-verhouding niet altijd letterlijk moet worden genomen. Het idee is vooral dat een klein deel van onze inspanning het grootste deel van de uitkomsten veroorzaakt.
De 80-20-regel is een zeer relevant instrument om verbeterkansen te prioriteren. Want een verbetering toepassen op een activiteit die 10.000 keer per jaar plaatsvindt, zelfs al is het maar een hele kleine, heeft vaak meer impact dan wanneer je een grote verbetering doorvoert op een activiteit die maar 3x per jaar plaatsvindt. Hetzelfde gaat op voor producten en diensten die je levert aan de klanten. Kortom, als consultant zet je jouw energie eerder op een paar producten die qua volume hoog zijn, dan op vele kleine producten of diensten.
Je kunt vele verschillende data analyseren met de 80-20 regel. Enkele voorbeelden die ik ben tegengekomen:
• 20% van de producten in een winkel zorgt voor 80% van de omzet
• 20% van je producten zorgt voor 80% van je consumentenklachten
• 20% van de werknemers zorgt voor 80% van de totale productie
• In 20% van de tijd lever je 80% van je werkresultaten
• 80% van het resultaat wordt bereikt met 20% van de input
Kortom, wil je een probleem aanpakken laat er altijd eerst een Pareto-analyse op los zodat je je focust op de grootste opbrengst!
Een scatter diagram is een grafiek die wordt gebruikt om de relatie tussen twee variabelen weer te geven. Het toont hoe de ene variabele verandert als de andere variabele verandert. Het wordt ook wel scatterplot of spreidingsdiagram genoemd en de eventuele samenhang tussen variabelen noemen we correlatie.
Het doel van het spreidingsdiagram is om patronen, trends, correlaties of afwijkingen in de gegevens te identificeren. Het kan helpen bij het bepalen van de aard van de relatie tussen de variabelen, of het nu positief, negatief of niet gecorreleerd is. Het diagram geeft direct een eerste indruk van eigenschappen van de data.
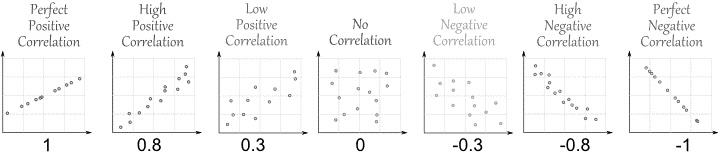
De Amerikaanse geiser Old Faithful barst elke circa 50 tot 80 minuten uit en blaast dan gedurende enkele minuten kokend water uit.
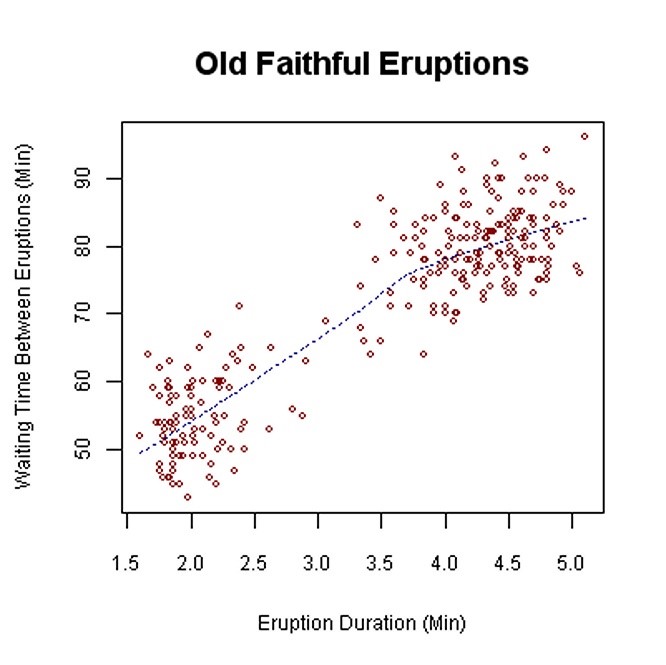
De puntenwolk laat duidelijk zien dat:
• er een verband is tussen de wachtduur en de uitbarstingsduur: hoe langer een uitbarsting op zich laat wachten, hoe langer deze zal duren;
• er twee aparte puntenwolken te zien zijn: eentje rond circa 2 minuten uitbarsting na 50 minuten wachten en eentje rond 4,5 minuten uitbarsting na 80 minuten wachten.
Let wel op! Je mag nooit zo maar uitgaan van het plaatje. Ik adviseer om altijd een meer formele statistische toets – bijvoorbeeld lineaire of niet-lineaire regressie - te gebruiken.
Het moge duidelijk zijn dat je hier dus data gebruikt waarvan jij aanneemt dat er een verband tussen is en dat je wilt nagaan hoe dat precies werkt. En waarschijnlijk zoek je dan naar een knop om aan te draaien om daarmee een gewenste verbetering te realiseren.
Je gebruikt alleen kwantitatieve data zoals temperatuur, leeftijd, duur, dat soort zaken. Het is belangrijk om te onthouden dat correlatie geen oorzakelijk verband impliceert. Hoewel twee variabelen gecorreleerd kunnen zijn, betekent dit niet noodzakelijkerwijs dat de ene variabele de andere veroorzaakt. Denk aan het bekende voorbeeld van ijsjes eten en aantal verdrinkingen. Die zullen een duidelijke positieve correlatie vertonen, maar de oorzaak ligt dus ergens anders, namelijk de buitentemperatuur.
Dus weet zeker dat je het onderwerp van jouw onderzoek goed inhoudelijk beheerst, anders kom je in het rijtje terecht: kleine leugens, grote leugens en statistieken!
Stratificatie, te vertalen als ‘laagvorming’, is het principe om een bepaalde populatie onder te verdelen in subpopulaties en deze subpopulaties afzonderlijk te bekijken. Kijk bijvoorbeeld naar onderstaand scatter diagram. Het toont met afwijkende symbolen in dezelfde grafiek de punten afkomstig uit de verschillende subpopulaties. Een gestratificeerde steekproef is de beste keuze als je denkt dat subgroepen verschillende gemiddelde waarden zullen hebben voor de variabele(n) die je bestudeert.
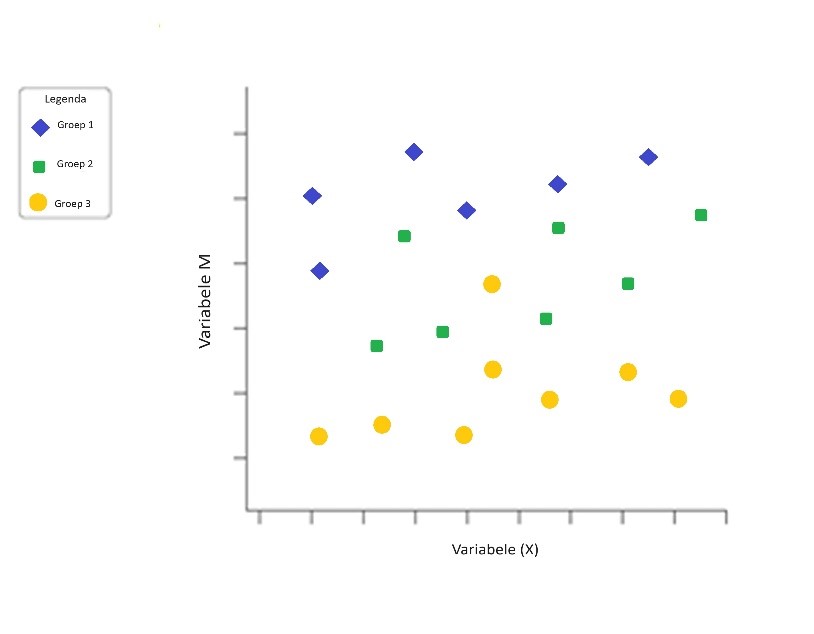
Je kunt zien dat het erop lijkt dat voor alle 3 de populaties er een lichte positieve correlatie is. Zoals al gezegd bij het scatter diagram moet je echter voorzichtig zijn met het trekken van die conclusie. Je ziet wel dat, wanneer je alle gegevens uit bovenstaand plaatje op een hoop zouden zijn gegooid, je alleen maar een willekeurige wolk zou zien.
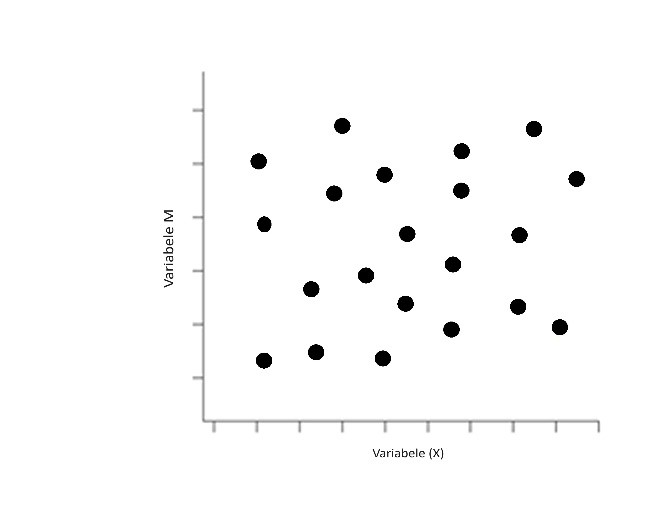
Dit toont ook direct het belang en de toepasbaarheid van stratificatie aan.
In een eerder plaatje in dit artikel had ik overigens ook veel beter stratificatie kunnen toepassen. Raad je welke?
Belangrijk is om, al voordat je data gaat het verzamelen, rekening te houden met de verschillende data die je tegen kunt komen in de bronnen die je onderzoekt. Als het zinvol is om onderscheid te maken tussen verschillende groepen van data zal ook de opzet van jouw dataverzameling specifieker moeten.
Vervolgens kun je de data in de verschillende tools die je gebruikt, visueel van elkaar scheiden bijvoorbeeld door middel van kleuren of symbolen. Je kunt de gestratificeerde data natuurlijk ook afzonderlijk visualiseren.
Analyseer de subsets van gestratificeerde gegevens afzonderlijk. In een spreidingsdiagram waarin gegevens zijn gestratificeerd in gegevens uit bron 1 en gegevens uit bron 2, teken je bijvoorbeeld kwadranten, tel je punten en bepaal je de kritische waarde alleen voor de gegevens uit bron 1, en vervolgens alleen voor de gegevens uit bron 2.
Stratificeren kun je gebruiken met allerlei verschillende datasets voor allerlei verschillende doelen. Om maar een volkomen willekeurig onderwerp te noemen, je zou een dataset waarin 2 verschillende prestatie-indicatoren zijn verwerkt (ik noem maar iets, producten met een doorlooptijd van 8 weken versus producten met een doorlooptijd van 13 weken) beter kunnen opsplitsen in 2 dataverzamelingen9.
Je kunt allerlei verschillende datasets stratificeren. Denk bijvoorbeeld aan productiecijfers gerelateerd aan ploegendiensten om te kijken welke ploegen beter produceren waarna je kunt onderzoeken hoe ze dat voor elkaar krijgen. Of we willen onderzoeken welke effecten thuiswerken heeft. Een ander voorbeeld is dat je op zoek gaat naar kwaliteitsverschillen tussen leveranciers. Of op welke dagen er meer fouten worden gemaakt door de medewerkers. Denk ook aan ziektes en medicijngebruik gestratificeerd naar bevolkingsgroep, om effectiever geneeskunde te bedrijven.
Ik heb stratificatie meerdere keren op persoonsniveau gedaan. Dat onderzoek deelde ik zelfs niet met de opdrachtgever vanwege privacyredenen maar ik kon toch regelmatig rapporteren dat er geen statistisch bewijs was dat het ene team beter presteerde dan het andere. In een geval heb ik geconstateerd dat een persoon met kop en schouders boven zijn collega’s uitstak. Ik heb daar toen dankbaar gebruik van gemaakt toen het ging om het opstellen van een ‘best practice’ procesbeschrijving.
De 7 Quality Tools zijn niet nieuw maar nog altijd actueel. In dit artikel heb ik aangegeven in welke situaties je ze goed kunt inzetten en hoe je daarbij data en data-analyse inzet om de tool goed te kunnen gebruiken. Ook heb ik iets verteld over de data die output zijn van de tool. Hiermee kun je verdergaan om de dienstverlening van jouw organisatie te verbeteren.
Eric Eggermont is gecertificeerd Master Black Belt Lean Six Sigma en co-founder van Lean Nederland. Het is zijn passie om bedrijven te ondersteunen bij het continu verbeteren van de dienstverlening.
Dit artikel is gebaseerd op een deel van hoofdstuk 7 van het recent uitgegeven boek ‘De Kwaliteit van Data’ van de sectie Data & Kwaliteit van het NNK. In 2018 richtte Arend Oosterhoorn de sectie Data en Kwaliteit van het NNK (Nederlands Netwerk voor Kwaliteitsmanagement) op. Onze missie is het gebruik van data en de bijdrage daarvan aan het leveren van kwaliteit in een snel veranderende omgeving voort- durend aanjagen en verbeteren. Een van de doelen was het publiceren over onze bevindingen. In de loop van 2020 ontstond het idee het verzamelde materiaal in een boek te verwerken. Arend heeft hieraan een belangrijke bijdrage geleverd. Na zijn overlijden begin 2022 heeft Kees de Vaal samen met de andere leden van de sectie het boek voltooid.
